Information and Process Modeling for Simulation – Part II: Activities and Processing Networks
This tutorial article is Part II of a series of three articles starting with Information and Process Modeling for Simulation – Part I: Objects and Events.
Copyright © 2019-2121 Gerd Wagner (CC BY-NC)
Published 2021-03-10. Also available as PDF.
Abstract
This article (1) reports new research results in the area of business process modeling and simulation, and (2) shows, in the style of a tutorial, how to use UML Class Diagrams and BPMN-style Process Diagrams for modeling Activities and Processing Networks. The state structure of a system is captured by a UML class model, which defines the types of objects, events and activities underlying a BPMN-style process model that captures the dynamics of the system in the form of a set of event rules. Part I of the tutorial presents the Object Event (OE) Modeling and Simulation (M&S) paradigm and the Discrete Event Process Modeling Notation (DPMN) as well as a basic OEM&S approach for modeling discrete event simulations (DES) with the help of OE class models and DPMN process models. In this second part, the basic OEM&S approach is extended by considering Activities and Processing Networks. Part III will show how to add the modeling concepts of Agents with Perceptions, Actions and Beliefs, resulting in a general agent-based Discrete Event Simulation modeling framework.
Table of Contents
List of Figures
- 1-1. A conceptual information model of a manufacturing workstation system
- 1-2. A conceptual process model of a manufacturing workstation system
- 1-3. An information design model
- 1-4. A process design model in the form of a DPMN Process Diagram
- 1-5. An ontology of the core categories of individuals of the OEM&S paradigm
- 1-6. A model of the core classes of individuals an OE simulator has to deal with at runtime.
- 1-7. A process design model in the form of a basic DPMN Process Diagram
- 1-8. An information design model in the form of a basic OE class model
- 1-9. A DPMN-A process model and its underlying OE class model
- 1-10. A DPMN-A process model with a resource-dependent activity start arrow and its underlying OE class model
- 1-11. A DPMN-A process model of a Load-Haul-Dump business process
- 1-12. A process design for the Make-and-Deliver-Pizza business process.
- 1-13. An enriched process design model
- 1-14. A process design for the Make-and-Deliver-Pizza business process.
- 2-1. Introducing an activity type in a conceptual information model of a single workstation system.
- 2-2. Introducing an activity type in a conceptual process model of a single workstation system.
- 2-3. Going from basic OEM to OEM-A class models by introducing activity types.
- 2-4. Going from basic DPMN to DPMN-A process models by introducing Activity rectangles.
- 2-5. Allocating the workstation as a resource of Processing activities
- 3-1. The resources required for performing an activity include the activity's performer.
- 3-2. Activity types may have special properties representing resource roles.
- 3-3. A conceptual information model of the activity type "examinations" with resource roles.
- 3-4. A conceptual process model based on the information model of Figure 3-3.
- 3-5. A conceptual information model with doctors and patients as people.
- 3-6. Adding the activity type "walks to room" to the conceptual information model.
- 3-7. A conceptual process model based on the information model of Figure 3-6.
- 3-8. An improved process model based on the information model of Figure 3-6.
- 3-9. Displaying the process owner and activity performers in a conceptual process model.
- 3-10. Adding parallel participation multiplicities for rooms participating both in walks and examinations at the same time.
- 3-11. An information model for the simplified design with the resource counters nmrOfRooms and nmrOfDoctors.
- 3-12. A process design model based on the information design model of Figure 3-11.
- 3-13. An OEM-A class model with resource object types for modeling resource roles and pools.
- 3-14. A process design model based on the information design model of Figure 3-13.
- 3-15. Any resource type R extends the pre-defined object type
Resource - 3-16. A simplified version of the model of Figure 3-13
- 3-17. An OE Class Diagram modeling a single workstation system with resource-constrained processing activities
- 3-18. An information design model for decoupling the allocation of rooms and doctors.
- 3-19. A process design model based on the information design model of Figure 3-18.
- 3-20. Representing the process owner as a Pool and activity performers as Lanes in a process design model.
- 3-21. A conceptual modeling pattern for a sequence of resource-constrained activities
- 3-22. Using resource-dependent activity start arrows in a conceptual process model.
- 3-23. Displaying the implicit allocate-release steps.
- 3-24. Modeling WorkStation as a resource type
- 3-25. A simplified version of the workstation process model using a resource-dependent activity start arrow.
- 3-26. A simplified version of the medical department information model with Doctor and Room as resource types
- 3-27. A simplified version of the medical department process model using resource-dependent activity start arrows.
- 4-1. Resource-constrained activities involving processing objects are processing activities.
- 4-2. A conceptual OEM class model defining built-in types for conceptual PN modeling
- 4-3. A PN model using the new DPMN modeling elements of PN Node rectangles and PN Flow arrows
- 4-4. A DPMN-PN process diagram with an Event Scheduling arrow
- 4-5. An OEM class design model defining built-in types for making PN design models
- 4-6. A PN model of a workstation system using PN Node rectangles and PN Flow arrows
- 4-7. A PN model of a workstation system where parts may have to be reworked
- 4-8. A PN model using the new DPMN modeling elements of PN Node rectangles and PN Flow arrows
- 4-9. An Arena diagram for the DMV model
- 4-10. An AnyLogic diagram for the DMV model (imposing Java naming syntax)
List of Tables
Chapter 1. Introduction
Object Event (OE) Modeling and Simulation (M&S) is a new general Discrete Event Simulation (DES) paradigm based on the two most important ontological categories: objects and events. In philosophy, objects have also been called endurants or continuants, while events have also been called perdurants or occurrents.
OEM&S combines Object-Oriented (OO) Modeling with the event scheduling paradigm of Event Graphs (Schruben 1983). The relevant object types and event types are described in an information model, which is the basis for making a process model. A modeling approach that follows the OEM paradigm is called an OEM approach. Such an approach needs to choose, or define, an information modeling language (such as Entity Relationship Diagrams or UML Class Diagrams) and a process modeling language (such as UML Activity Diagrams or BPMN Process Diagrams).
We propose an OEM approach based on UML Class Diagrams for conceptual information modeling and information design modeling, as well as DPMN Process Diagrams for conceptual process modeling and for process design modeling.
In the proposed approach, object types and event types are modeled as special categories of classes in a UML Class Diagram. Random variables are modeled as a special category of class-level operations constrained to comply with a specific probability distribution such that they can be implemented as static methods of a class. Queues are not modeled as objects, but rather as ordered association ends, which can be implemented as collection-valued reference properties. Finally, event rules, which include event routines, are modeled in DPMN process diagrams (and possibly also in pseudo-code), such that they can be implemented in the form of special onEvent methods of event classes.
Like Petri Nets and DEVS, OEM&S has a formal semantics. But while Petri Nets and DEVS are abstract computational formalisms without an ontological foundation, OEM&S is based on the ontological categories of objects, events and causal regularities.
An OEM approach results in a simulation design model that has a well-defined operational semantics in terms of a transition system based on the event rules modeled in a DPMN process design diagram, as shown by Wagner (2017a). Such a model can, in principle, be implemented with any object-oriented (OO) simulation technology. However, a straightforward implementation can only be expected from a technology that implements the OEM&S paradigm, such as the OES JavaScript (OESjs) framework.
Both conceptual models for DES and DES design models consist of (1) an information model and (2) a process model. In the case of conceptual modeling, an information model describes the types of objects and events representing the main entities of the real-world system under investigation, while a process model describes its dynamics in the form of a set of conceptual event rule models that capture the causal regularities of the system.
In the case of simulation design modeling, an information design model defines the types of all objects and events that are relevant for the purpose of a simulation study, thus defining the state structure of a DES system, while a process design model defines the dynamics of a DES system by defining, for all event types of the underlying information model, an event rule design model that specifies the state changes and follow-up events implied by the occurrence of an event of that type.
In the first part of this article series, (Wagner 2018b), we have introduced a variant of the Business Process Modeling Notation (BPMN), called Discrete Event Process Modeling Notation (DPMN), and have shown how to use UML Class Diagrams and DPMN Process Diagrams for making basic OE models defining a set of object types OT, a set of event types ET, and a set of event rules R. In (Wagner 2017a), we have shown that (a) these three sets define a state transition system, where the state space is defined by OT and ET, and the transitions are defined by R, and (b) such a transition system represents an Abstract State Machine in the sense of Gurevich (1985). This fundamental characterization of an OE model provides a formal (operational) semantics for OE Simulation (OES) by defining an OES formalism that any OE simulator has to implement.
In this second part, we extend basic OEM/DPMN in two steps by adding support for (1) resource-constrained activities and (2) GPSS/SIMAN/Arena-style processing activities and processing networks (PNs).
Modeling resource-constrained activities has been a major issue in DES since its inception in the nineteen-sixties, while it has been neglected and is still considered an advanced topic in the field of Business Process Modeling (BPM). BPMN only provides partial support for modeling resource-constrained activities. It allows assigning resources to activities, but it does not allow modeling resource pools, and it does neither allow specifying resource cardinality constraints nor parallel participation multiplicity constraints.
Processing objects enter PNs via arrival events at an entry node and then flow through one or more processing nodes where they are subject to processing activities before they leave the system at an exit node via a departure event. The first extension, OEM/DPMN-A, comprises five new information modeling categories ("stereotypes") and one new process modeling element, while the second extension, OEM/DPMN-PN, comprises a set of four pre-defined object types and three pre-defined event types, three new (node type) categories and one new process modeling element, as listed in tables in Appendix A: OEM Elements.
1.1. Object Event Modeling
1.1.1. Example: A Manufacturing Workstation Model
A manufacturing workstation receives parts and stores them in its input buffer for processing them successively.
Conceptual Model
A conceptual information model of a workstation system, defining two object types and four event types, is shown in Figure 1-1.
As expressed by the associations between the four event types and the two object types, for all four types of events, there are the same two types of objects participating in them: parts and workstations, implying that each event of these four types involves a specific part and a specific workstation.
Notice that the input buffer (filled with waiting parts) is modeled as an association end with name waiting parts at the parts side of the association between parts and workstations, expressing the fact that at any point in time, a workstation has zero or more parts waiting in its input buffer for being processed.
A conceptual process model of this system, describing four causal regularities in the form of event rules, one for each type of event, is shown in Figure 1-2 in the form of a BPMN Process Diagram using Event circles connected with Sequence Flow arrows expressing (conditional) causation, and Data Objects attached to Event circles.
The four event rules described by this model are
- When a part arrives, it is added to the input buffer and, if the workstation is available, there will be a processing start event for processing the newly arrived part.
- When a processing start event occurs, the next part from the input buffer is being processed and a processing end event is caused to occur some time later (after the processing time has elapsed).
- When a processing end event occurs, this will cause a part departure event and, if the input buffer is not empty, another processing start event involving the next part from the buffer.
- When a part departure event occurs, the processed part will be removed from the workstation.
Design Model
A simulation design model is based on a conceptual model. Depending on the purposes/goals of a simulation study, it may abstract away from certain elements of the real-world domain described by the conceptual model, and it adds computational elements representing design decisions, such as random variables expressed int he form of random variate sampling functions based on specific probability distributions for modeling the random variation of certain system variables.
An information design model of the single workstation system described above is shown in Figure 1-3. This model defines the multi-valued waitingParts association end to be ordered, which means that it corresponds to a multi-valued reference property holding an ordered collection (such as an array list or a queue) as its value.
The information design model of Figure 1-3 defines that a PartArrival event must reference both a Part and a WorkStation, representing situations where specific parts arrive at specific workstations. Notice that, computationally, this model requires creating new Part objects (or retrieving them from an object pool) before a new PartArrival event is created (or scheduled), while it is more common in simulation models to create a new Part object only when an arrival event has occurred, which can be modeled by defining a multiplicity of 0..1 for the Part end of the PartArrival-Part association (with the meaning that PartArrival has an optional, instead of a mandatory, reference property with name part).
Notice that the model defines two class level operations (designated with the stereotype «rv») implementing random variate sampling functions: PartArrival::recurrence() complies with a triangular probability distribution with minimum, mode and maximum parameter values 3, 4 and 8, while ProcessingStart::processingTime() complies with an exponential distribution with a mean of 6.
A process design model based on the object and event types defined by the information design model of Figure 1-3 and derived from the conceptual process model of Figure 1-2 is shown in Figure 1-4.
Notice that, since all events happen at the same workstation, all three event scheduling arrows are annotated with the same event property assignment workStation := ws, which simply propagates the object reference to the given workstation along the event scheduling chain. Such property propagation assignments (in event property assignment annotations), where a property value of a follow-up event is set to the corresponding property value of the scheduling (or triggering) event, will be omitted (as implied by event types having the same property names) for avoiding to clutter the process model diagrams.
A DPMN Process Diagram, like the one shown in Figure 1-4, can be split up into a set of event rule diagrams, one for each of its Event circles, as shown in the following table. This reduction of a DPMN process design model to a set of event rule design models, together with the operational semantics of event rules presented in (Wagner 2017a), provides the semantics of DPMN Process Diagrams.
Notice that an event rule design model can also be expressed textually in the form of a pseudo-code block with four parts: part 1 indicates the triggering event type and declares a rule variable representing the triggering event, part 2 declares further rule variables and initializes them, part 3 contains a state change script consisting of state change statements, and part 4 schedules follow-up events.
| Rule design model | Pseudo-code | ||||
|---|---|---|---|---|---|
| |||||
| |||||
|
1.2. Ontological Considerations
Ontologically, an activity is a composite event (composed of at least a start and an end event) with a duration greater than zero, performed by an agent (a human or another living being, a robot or another artificial agent, or an organization or another social agent). As opposed to activities, activity start and end events are instantaneous (zero-duration) events.
As an event, an activity has objects that participate in it. In the real world, an activity has at least one participant: the performer of the activity. Consequently, a conceptual model should, for each activity type, include the type of objects that play the performer role for activities of that type, as described by the UML class diagram shown in Figure 1-5.
However, in a simulation design model we may choose to leave the performer of an activity implicit and model an activity without modeling any participant. Consequently, a basic OE simulator, the core classes of which are described in Figure 1-6, does not need to support the distinction between objects and agents.
1.3. Object Event Simulation
The Object Event Simulation (OES) paradigm is an extension of the Event-Based Simulation (ES) paradigm pioneered by SIMSCRIPT (Markowitz, Hausner & Karr 1962) and later formalized by Event Graphs (Schruben 1983). Essentially, OES extends ES, or Event Graphs, by adding the modeling concepts of objects and event rules.
Starting with an initial simulation state, an OE model is executed by successively applying the event rules of the model to the evolving simulation states.
Notice that the occurrence time of an activity is the time when it completes, that is, it is equal to startTime + duration. Typically, the duration of an activity in a simulation run is known, and set, when it is started. An activity type is normally defined with a fixed duration or a random variable duration for all activities of that type. This allows a simulator to schedule the activity's end event when the activity is started. However, in certain cases, an activity type may not define a preset duration, but leave the duration of activities of that type open. When such an activity is still ongoing, it does only have a start time, but no duration and no occurrence time.
The OES formalism
The OEM&S paradigm is based on the OES formalism presented in (Wagner 2017a), which is summarized below.
Both object types and event types are defined in the form of classes: with a name, a set of properties and a set of operations, which together define their signature. A property is essentially defined by a name and a range, which is either a datatype (like Integer or String) or another object type.A set of object types OT defines a predicate-logical signature as the basis of a logical expression language LOT: each object type defines a unary predicate, and its properties define binary predicates. A state change language COT based on OT defines state change statements expressed with the help of the object type names and property names defined by OT. In the simplest case, state change statements are property value assignments like o.p1 := 4 or o.p1 := o.p2 where o is an object variable and p1, p2 are property names.
A set of objects O = {o1, o2, ...on} where each of them has a state in the form of a set of slots (property-value pairs) represents a system state, that is a state of the real-world system being modeled and simulated. A system state O can be updated by a set of state changes (or, more precisely, state change statements) Δ ⊆ COT with the help of an update operation Upd. For instance, for a system state O1 = {o1} with o1 = { p1: 2, p2: 5} and a set of state changes Δ1 = { o1.p1 := o1.p2 } we obtain
An event expression is a term E(x)@t where
- E is an event type,
- x is a (possibly empty) list of event parameters x1, x2, …, xn according to the signature of the event type E,
- t is a parameter for the occurrence time of events.
For instance, PartArrival(ws)@t is an event expression for describing part arrival events where the event parameter ws is of type WorkStation, and t denotes the arrival time. An individual event of type E is a ground event expression, e = E(v)@i, where the event parameter list x and the occurrence time parameter t have been instantiated with a corresponding value list v and a specific time instant i. For instance, PartArrival(ws1)@1 is a ground event expression representing an individual PartArrival event occurring at workstation ws1 at time 1.
A Future Events List (FEL) is a set of ground event expressions partially ordered by their occurrence times, which represent future time instants either from a discrete or a continuous model of time. The partial order implies the possibility of simultaneous events, as in the example {ProcessingEnd(ws1)@4, PartArrival(ws1)@4}.An event routine is a procedure that essentially computes state changes and follow-up events, possibly based on conditions on the current state. In practice, state changes are often directly performed by immediately updating the objects concerned, and follow-up events are immediately scheduled by adding them to the FEL. For the OES formalism, we assume that an event routine is a pure function that computes state changes and follow-up events, but does not apply them, as illustrated by the examples in the following table.
Event rule name / rule variables | ON (event expression) | DO (event routine) |
rPA a: PartArrival | PartArrival(ws) @ t | Δ := { ws.waitingParts.push( a.part)} IF ws.status = AVAILABLE RETURN ⟨ Δ, FE ⟩ |
rPS ps: ProcessingStartws: WorkStation ws := ps.workStation | ProcessingStart(ws) @ t | Δ := { ws.status := BUSY} FE := {ProcessingEnd(ws)@t + ProcessingStart.processingTime()} RETURN ⟨ Δ, FE ⟩ |
rPE pe: ProcessingEndws: WorkStation ws := pe.workStation | ProcessingEnd(ws) @ t | Δ := { ws.waitingParts.pop()} IF ws.waitingParts.length > 0 RETURN ⟨ Δ, FE ⟩ |
An event rule associates an event expression with an event routine F:
where the event expression E(x)@t specifies the type E of events that trigger the rule, and F( t, x) is a function call expression for computing a set of state changes and a set of follow-up events, based on the event parameter values x, the event's occurrence time t and the current system state, which is accessed in the event routine F for testing conditions expressed in terms of state variables.
An OE model based on a state change language COT and a corresponding update operation Upd is a triple ⟨OT, ET, R⟩, consisting of a set of object types OT, event types ET and event rules R.
An OE simulation (system) state based on an OE model ⟨OT, ET, R⟩ is a triple S = ⟨t, O, E⟩ with t being the current simulation time, O being a system state (a set of objects instantiating types from OT), and E being a set of imminent events to occur at times greater than t (and instantiating types from ET), also called Future Event List (FEL).An event rule r = ON E(x)@t DO F( t, x) can be considered as a 2-step function that, in the first step, maps an event e = E(v)@i to a parameter-free state change function re = F( i, v), which maps a system state O to a pair ⟨ Δ, FE ⟩ of system state changes Δ ⊆ COT and follow-up events FE. When the parameters t and x of F( t, x) are replaced by the values i and v provided by a ground event expression E(v)@i, we also simply write Fi,v instead of F( i, v) for the resulting parameter-free state change function.
We say that an event rule r is triggered by an event e when the event's type is the same as the rule's event type. When r is triggered by e, we can form the state change function re = Fi,v and apply it to a system state O by mapping it to a set of state changes and a set of follow-up events:
We can illustrate this with the help of our workstation example. Consider the rule rPA defined in the table above triggered by the event PartArrival(ws1)@1 in state O0 = {ws1.status: AVAILABLE, ws1.waitingParts: []}. We obtain
with Δ1 = { ws1.waitingParts.push( a.part)} and FE1 = {ProcessingStart@2}.
An OE model defines a state transition system where
A state is a simulation state S = ⟨t, O, E⟩.
A transition of a simulation state S consists of
advancing t to the occurrence time t' of the next events NE ⊆ E, which is the set of all imminent events with minimal occurrence time;
processing all next events e ∈ NE by applying the event rules r ∈ R triggered by them to the current system state O according to
re( O ) = ⟨ Δe , FEe ⟩resulting in a set of state changes Δ = ∪ {Δe | e ∈ NE } and a set of follow-up events FE = ∪ {FEe | e ∈ NE }.
such that the resulting successor simulation state is S' = ⟨ t', O', E' ⟩ with O' = Upd( O, Δ) and E' = E − NE ∪ FE.
Notice that the OES formalism first collects all state changes brought about by all the simultaneous next events (from the set NE) of a simulation step before applying them. This prevents the state changes brought about by one event from NE to affect the application of event rules for other events from NE, thus avoiding the problem of non-determinism through the potential non-confluence (or non-serializability) of parallel events.
OE simulators are computer programs that implement the OES formalism. Typically, for performance reasons, discrete event simulators do not first collect all state changes brought about by all the simultaneous next events (the set NE) of a simulation step before applying them, but rather apply them immediately in each triggered event routine. However, this approach takes the risk of an unreliable semantics of certain simulation models in favor of performance.
OESjs – a JavaScript-based OE simulator
The OESjs simulator presented in (Wagner 2017b) implements the OES formalism by implementing (1) object types as classes extending the pre-defined class oBJECT, (2) event types as classes extending the pre-defined class eVENT, and (3) event rules as onEvent methods of event classes.
The OESjs simulator is available from the educational simulation website sim4edu.com.
1.4. Discrete Event Processes, Business Processes and Processing Processes
A discrete event process consists of a partially ordered set of events that cause a corresponding sequence of discrete state changes of affected objects. When two or more events within such a process have the same order rank, this means that they occur simultaneously. A discrete event process, also known more simply as a discrete process, may be an instance of a discrete process type defined by a discrete process model.
A business process is a discrete process that serves certain business purposes of an organization and involves events and activities performed by actors of the organization. Typically, a business process is an instance of a business process type defined by an organization (or organizational unit), which is the owner of the business process type, in the form of a business process model.
A business process model defines an Activity Network (AN) consisting of event and activity nodes connected by means of event flow arrows and resource-dependent activity scheduling (RDAS) arrows, such that event and activity nodes may be associated with objects representing their participants. In the case of an activity node, these participating objects include the resource objects required for performing an activity. Typically, an activity node is associated with a particular resource object representing the activity performer.
An RDAS arrow from an activity node (or an event) to a successor activity node expresses the fact that a corresponding activity end event (or plain event) triggers the conditional scheduling of a successor activity start event, corresponding to the creation of a new task in the task queue of (the performer of) the successor activity.
An activity node of an AN typically has a queue of tasks (or planned activities) waiting for the availability of the required resources.
A processing process is a business process involving arrival events, processing activities and departure events. An arrival event for one or more processing objects happens at an entry station, from where they are routed to a processing station where processing activities are performed on them, before they are routed to another processing station or to an exit station where they leave the system via a departure event.
A processing process model defines a Processing Network (PN) consisting of entry nodes, processing nodes and exit nodes where each node represents a combination of a spatial object and an event type:
- Defining an entry node means defining both an entry station object (e.g., a reception area or a factory entrance) and an arrival event type for arriving processing objects (such as people or manufacturing parts).
- Defining a processing node means defining both a processing station object (often used as a resource object, such as a workstation or a room) and a processing activity type.
- Defining an exit node means defining both an exit station object and a departure event type.
In a PN, all processing nodes have an input buffer (or queue) filled with processing objects that wait to be processed. A PN where all processing activities have exactly one abstract resource (a "server") is also known as a Queuing Network in Operations Research (where processing nodes are called "servers" and processing objects are called "entities" or "jobs").
For accommodating resource-constrained activities and Processing Networks, basic OEM and DPMN are extended in two steps. The first extension, OEM/DPMN-A, comprises four new information modeling categories (activity types, resource roles, resource pools, and parallel participation) and one new process modeling element (RDAS arrows), while the second extension, OEM/DPMN-PN, comprises a set of four pre-defined object type categories (processing objects, entry stations, processing stations, exit stations), two pre-defined event type categories (arrival events, departure events), one activity type category (processing activities), three node type categories (entry nodes, processing nodes, exit nodes) and one new process modeling element (object flow arrows).
A. Discrete Event Processes and Event Graphs
A discrete event process consists of a partially ordered set of events that cause a corresponding sequence of discrete state changes of affected objects. When two or more events within such a process have the same order rank, this means that they occur simultaneously.
As an example of a discrete event process we consider a manufacturing process with a workstation and three types of events: PartArrival events, ProcessingStart events and ProcessingEnd events.
The example process is described by the following list of event expressions: PartArrival@1, [email protected], [email protected], [email protected], [email protected], [email protected], [email protected], [email protected], [email protected], where an expression E@t represents an event of type E occurring at time t.
How this process unfolds in time is illustrated by the following process log:
| Step | Time | System State | Future Events |
|---|---|---|---|
| 0 | 0 | WorkStation-1{ bufLen: 0, status: "AVAILABLE"} | PartArrival@1 |
| 1 | 1 | WorkStation-1{ bufLen: 1, status: "AVAILABLE"} | [email protected], [email protected] |
| 2 | 1.01 | WorkStation-1{ bufLen: 1, status: "BUSY"} | [email protected], [email protected] |
| 3 | 5.4 | WorkStation-1{ bufLen: 2, status: "BUSY"} | [email protected], [email protected] |
| 4 | 6.5 | WorkStation-1{ bufLen: 3, status: "BUSY"} | [email protected] |
| 5 | 8.47 | WorkStation-1{ bufLen: 2, status: "BUSY"} | [email protected] |
| 6 | 8.48 | WorkStation-1{ bufLen: 2, status: "BUSY"} | [email protected] |
| 7 | 11.95 | WorkStation-1{ bufLen: 1, status: "BUSY"} | [email protected] |
| 8 | 11.96 | WorkStation-1{ bufLen: 1, status: "BUSY"} | [email protected] |
| 9 | 17.48 | WorkStation-1{ bufLen: 0, status: "AVAILABLE"} |
The events of a real-world discrete event process happen in a coherent spatio-temporal region determined by the locations of the events' participants. In a simulation model, one may abstract away from the aspect of space and model objects without locations, implying that events and processes happen in time, but not in space.
A discrete event process, also known more simply as a discrete process, may be an instance of a discrete process type defined by a discrete process model. A discrete event process pattern can be modeled in the form of a basic DPMN process diagram, which is an extended Event Graph.
The Event Graph modeling language proposed by Schruben (1983) defines directed graphs where the nodes are Event circles (representing typed event variables) annotated with state change statements in the form of state variable assignments, and the edges are arrows representing event flows. In the case of a conceptual process model, event flow arrows express the causation of follow-up events. In the case of a process simulation design model, event flow arrows express the scheduling of follow-up events according to the event scheduling paradigm of Discrete Event Simulation.
Basic DPMN extends the Event Graph diagram language by adding object rectangles containing declarations of typed object variables and state change statements, as well as gateway diamonds for expressing conditional and parallel branching.
The following basic DPMN diagram is an extended Event Graph defining a process pattern that is instantiated by the above discrete event process example.
This process model is based on the following Object Event (OE) class model:
A DPMN process design model specifies a set of chained event rules, one rule for each Event circle of the model. The above model specifies the following three event rules:
- On each PartArrival event, the inputBufferLength attribute of the associated WorkStation object is incremented and if the workstation's status attribute has the value AVAILABLE, then a new ProcessingStart event is scheduled to occur immediately.
- When a ProcessingStart event occurs, the associated WorkStation object's status attribute is changed to BUSY and a ProcessingEnd event is scheduled with a delay provided by invoking the processingTime function defined in the ProcessingStart event class.
- When a ProcessingEnd event occurs, the inputBufferLength attribute of the associated WorkStation object is decremented and if the inputBufferLength attribute has the value 0, the associated WorkStation object's status attribute is changed to AVAILABLE. If the inputBufferLength attribute has a value greater than 0, a new ProcessingStart event is scheduled to occur immediately.
The formal (transition system) semantics of basic DPMN diagrams, based on the semantics of event rules as transition functions, has been presented in (Wagner 2017a). It can be shown that the basic DPMN diagram language is a conservative extension of the Event Graph diagram language by means of a homomorphic embedding of Event Graphs in DPMN diagrams.
B. Business Processes and Activity Networks
An activity is a composite event that is composed of, and temporally framed by, a pair of start and end events.
A business process of an organization is a discrete event process that includes activities performed by actors of the organization for serving certain business purposes of the organization. In addition to its performer, an activity may involve further resources, and allocating the required resources from resource pools during the course of a business process is essential for keeping it going.
As an example of a business process we consider a manufacturing process with a workstation and three types of events: PartArrival events, Processing-Activity-Start events and Processing-Activity-End events.
The example business process is described by the following list of event expressions: PartArrival@1, [email protected], [email protected], [email protected], [email protected], [email protected], [email protected], [email protected], [email protected], where an expression E@t represents an event of type E occurring at time t.
How this process unfolds in time is illustrated by the following process log:
| Step | Time | System State | Future Events |
|---|---|---|---|
| 0 | 0 | WorkStation-1{ status: 1} | av. workStations: ws1 | PartArrival@1 |
| 1 | 1 | WorkStation-1{ status: 2} | av. workStations: | Processing-Activity-Start{ ws1 }@1.01, [email protected] |
| 2 | 1.01 | WorkStation-1{ status: 2} | av. workStations: | Processing-Activity-End{ ws1 }@8.08, [email protected] |
| 3 | 8.08 | WorkStation-1{ status: 1} | av. workStations: ws1 | [email protected] |
| 4 | 18.83 | WorkStation-1{ status: 2} | av. workStations: | Processing-Activity-Start{ ws1 }@18.84, [email protected] |
| 5 | 18.84 | WorkStation-1{ status: 2} | av. workStations: | Processing-Activity-End{ ws1 }@23.9, [email protected] |
| 6 | 23.9 | WorkStation-1{ status: 1} | av. workStations: ws1 | [email protected] |
| 7 | 25.61 | WorkStation-1{ status: 2} | av. workStations: | Processing-Activity-Start{ ws1 }@25.62 |
| 8 | 25.62 | WorkStation-1{ status: 2} | av. workStations: | Processing-Activity-End{ ws1 }@32.03 |
| 9 | 32.03 | WorkStation-1{ status: 1} | av. workStations: ws1 |
Notice that, as opposed to the process log shown in Table 1-1,
- the workstation with ID 1 is a (performer) resource for Processing activities having either the status 1 (being available) or 2 (being busy), and
- there is a pool of available resources ("av. workStations").
Typically, a business process is an instance of a business process type defined by an organization (or organizational unit), which is the owner of the business process type, in the form of a business process model. The above example business process is an instance of the following model:
A business process model defines an Activity Network (AN), which provides a pattern for business processes. An AN specifies a set of chained event rules with typed object, event and activity variables, based on an OE class model defining object, event and activity types. By convention, activity classes have a duration function that is invoked for getting the duration of newly created instances of the activity class. In a simulation design model, these functions typically define random variate sampling functions (like the service time concept in queuing theory).
Event circles and Activity rectangles may be connected via event flow arrows, as shown above in Figure 1-9, or via resource-dependent activity scheduling arrows, as shown below in Figure 1-10.
The AN shown in Figure 1-9 defines the following event rules:
- On each PartArrival event, if the associated WorkStation object's status attribute has the value AVAILABLE, then it is set to BUSY and the rule variable wsAllocated is set to true; otherwise the inputBufferLength attribute of the associated WorkStation object is incremented. If wsAllocated holds, then a new Processing activity is scheduled to start immediately with a duration provided by invoking the duration function defined in the Processing activity class.
- When a Processing activity ends, if the inputBufferLength attribute of the associated WorkStation object has the value 0, then the WorkStation object's status attribute is set to AVAILABLE; otherwise the rule variable wsAllocated is set to true and the WorkStation object's inputBufferLength attribute is decremented. If wsAllocated holds, then a new Processing activity is scheduled to start immediately with a duration provided by invoking the duration function defined in the Processing activity class.
Since the resource management logic concerning the workstation as a resource for Processing activities follows a general pattern, a new modeling language element can be introduced for capturing this pattern. Using resource-dependent activity start arrows, we can express the process model of Figure 1-9 more simply as in the following diagram:
Notice that in this model, we have expressed that we no longer have to take care of setting the status of the workstation as a resource, nor do we have to update the queue/buffer length. This is now expressed implicitly by the semantics of the resource-dependent activity scheduling (RDAS) arrow and has to be handled in a generic way by a simulator supporting DPMN-A models.
The following diagram shows a model containing both event scheduling arrows and RDAS arrows:
In this model, activities are initiated (1) by an RDAS arrow when they may have to wait for the availability of required resources, or (2) by an event scheduling arrow when no other resources are required. For instance, a new Load activity can only be started, when a wheel loader (as a performer) is available, while a Haul activity can be started immediately after the completion of a Load activity because it's performed by the loaded truck, and no other resources are required.
The most widely used language for defining ANs is the Business Process Modeling Notation (BPMN). However, in BPMN there is only one type of arrow, called "Sequence Flow", which is semantically overloaded with both meanings: it can represent an event flow arrow or a resource-dependent activity start arrow.
The concept of ANs includes business system processes, where many business actors perform activities for handling many business cases in parallel. Consequently, it is more general than the common concept of a business process as a case-handling process.
Normally all activity nodes of an AN have a queue of planned activities ("tasks") waiting for the availability of required resources (in particular, their performer). Only if a successor activity node does not require additional or different resources, it does not have a (resource allocation) queue and can be started right away whenever a predecessor activity has completed, as indicated by an event flow arrow.
When all activity nodes of an AN only have a single resource (the performer of the activity), and each of them has a different performer, then the AN corresponds to a Queuing Network in the sense of Operations Research.
A DPMN process design model (like the one shown in Figure 1-12) essentially defines the admissible sequences of events and activities together with their dependencies and effects on objects, while its underlying OE class design model (like the one shown in Figure 1-14 below) defines the types of objects, events and activities, together with the participation of objects in events and activities, including the resource roles of activities, as well as resource cardinality constraints, parallel participation constraints, alternative resources, and task priorities.
It is an option, though, to enrich a DPMN process design model by displaying more computational details, especially the recurrence of exogenous events, the duration of activities and the most important resource management features defined in the underlying OE class design model, such as resource roles (in particular, performer roles can be displayed in the form of Lanes), resource cardinality constraints, alternative resources, and task priorities. The following model shows an enriched version of Figure 1-12:
Such an enriched DPMN process design model includes all computational details needed for an implementation without a separate explicit OE class design model. In fact, such a process model implicitly defines a corresponding class model. For instance, the enriched DPMN model of Figure 1-13 above implicitly defines the following OE class model:
C. Processing Processes and Processing Networks
T.B.D.
Chapter 2. Simple Activities
A simple activity is an activity with zero or more participants, none of which is having a special meaning (such as being a resource or a processing object).
2.1. Conceptual Modeling of Simple Activities
Conceptually, an activity is a composite event that is composed of, and temporally framed by, a pair of start and end events. Consequently, whenever a model contains a pair of related start and end event types, like processing start and processing end in the model of a manufacturing workstation shown on the left-hand side of Figure 2-1 and Figure 2-2, they can be replaced with a corresponding activity type, like processing, as shown on the right-hand side.
It is obvious that applying this replacement pattern leads to a conceptual and visual simplification of the models concerned.
2.2. Design Modeling of Simple Activities
Like in a conceptual model, also in a design model, a pair of corresponding activity start Event and end Event circles, like ProcessingStart and ProcessingEnd in the source models shown in Figure 2-3 and Figure 2-4, can be replaced with a corresponding Activity rectangle, like Processing, as in the target models shown in these figures.
Extending basic OEM information design models by adding activity types
In the case of an information design model, this replacement pattern implies allocating all features (attributes, associations and operations) of the classes defining the start and the end event type in the class defining the corresponding activity type, possibly with renaming some of them. In the example of Figure 2-3, there is only one such feature: the class-level operation ProcessingStart::processingTime, which is allocated to Processing and renamed to time.
Extending basic DPMN process design diagrams by adding Activity rectangles
In the case of a process design model, the replacement pattern implies that an Event circle pair consisting of an Event circle intended to represent activity start events and an Event circle intended to represent related activity end events, with an event scheduling arrow from the start to the end Event circle annotated by a delay expression, is replaced by an Activity rectangle such that:
- All Data Objects attached to the end Event circle get attached to the Activity rectangle (since an activity occurs when it it is completed).
- All event scheduling arrows going out from the end Event circle are turned into event scheduling arrows going out from the Activity rectangle.
- All start event scheduling arrows are replaced with corresponding activity scheduling arrows having an additional creation parameter assignment for the duration of a scheduled activity, which is set to the delay expression defined for the end event scheduling arrow. In the example above, the duration parameter in the annotation of the two activity scheduling arrows is set to
Processing::time()in the target diagram, which is the same as the delayProcessingStart::processingTimein the source diagram. - When the start Event circle has one or more attached Data Objects or any outgoing event scheduling arrow that does not go to the end Event circle, then a start Event circle has to be included in the Activity rectangle for attaching the Data Object(s) and as the source of the outgoing event scheduling arrow(s).
This Activity-Start-End Rewrite Pattern, which can also be applied in the inverse direction, replacing an Activity rectangle with an Event circle pair, defines the meaning of an Activity rectangle in a DPMN diagram. It allows reducing a DPMN-A diagram with Activity rectangles to a basic DPMN diagram without Activity rectangles.
Notice that, like the source model, also the target model of Figure 2-4 specifies three event rules:
- On each PartArrival event, the arrived part is added to the workstation's input buffer and if the workstation's status is AVAILABLE, then a new Processing activity is scheduled to start immediately with a duration provided by invoking the time function defined in the Processing activity class.
- When a Processing activity starts, the workstation's status is changed to BUSY.
- When a Processing activity ends, the processed part is removed from the input buffer and, if the input buffer is not empty, a new Processing activity is scheduled to start immediately, otherwise (if the input buffer is empty) the workstation's status is changed to AVAILABLE.
An alternative process design model of the single workstation system
Based on the same information design model, shown in Figure 2-3, we can make another process design model of the single workstation system as an alternative to the target model of Figure 2-4. This alternative model makes it more clear that a workstation is, in fact, an exclusive resource of its processing activity. The concepts of resources and resource-constrained activities are discussed in the following sections, and in Section 3.2, it is shown how to simplify the basic DPMN model of Figure 2-5 by using the higher-level modeling elements introduced in DPMN-A.
Chapter 3. Resource-Constrained Activities
A Resource-Constrained Activity is an activity where one or more participants play a Resource Role (such as Performer). Typically, a resource-constrained activity is a component of a business process that happens in the context of an organization or organizational unit, which is associated with the activity as its Process Owner.
An activity of a certain type may require certain resources for being performable. At any point in time, a resource required for performing an activity may be available or not. A resource is not available, for instance, when it is is busy or when it is out of order.
Resources are objects of a certain type. The resource objects of an activity include its performer, as expressed in the diagram shown in Figure 3-1. While in a conceptual model, describing a real-world system, a performer is required for any activity, a simulation design model may abstract away from the performer of an activity.
For instance, a consultation activity may require a consultant and a room. Such resource cardinality constraints are defined at the type level. When defining the activity type Consultation, these resource cardinality constraints are defined in the form of two mandatory associations with the object types Consultant and Room such that both associations' ends have the multiplicity 1 ("exactly one"). Then, in a simulation run, a new Consultation activity can only be started, when both a Consultant object and a Room object are available.
For all types of resource-constrained activities, a simulator can automatically collect the following statistics:
- Throughput statistics: the numbers of enqueued and dequeued planned activities, and the numbers of started and completed activities.
- Queue length statistics (average, maximum, etc.) of its queue of planned activities.
- Cycle time statistics (average, maximum, etc.), where cycle time is the sum of the waiting time and the activity duration.
- Resource utilization statistics: the percentage of time each resource object involved is busy with an activity of that type.
In addition, a simulator can automatically collect the percentage of time each resource object involved is idle or out-of-order.
For modeling resource-constrained activities, we need to define their types. As can be seen in Figure 3-2, a resource-constrained activity type is composed of
- a set of properties and a set of operations, as any entity type,
- a set of resource roles, each one having the form of a reference property with a name, an object type as range, and a multiplicity that may define a resource cardinality constraint like, e.g., "exactly one resource object of this type is required" or "at least two resource objects of this type are required".
The resource roles defined for an activity type may include the performer role.
These considerations show that a simulation language for simulating activities needs to allow defining activity types with two kinds of properties: ordinary properties and resource roles. At least for the latter ones, it must be possible to define multiplicities for defining resource cardinality constraints. These requirements are fulfilled by OE Class Diagrams where resource roles are defined as stereotyped properties using the stereotype «resource role» or, shorter, «res».
The extension of basic OEM by adding the concepts needed for modeling resource-constrained activities (in particular, resource roles with constraints, resource pools, and resource-dependent activity start arrows) is called OEM-A.
3.1. Conceptual Modeling of Resource-Constrained Activities
Modeling resource-constrained activities has been a major issue in the field of Discrete Event Simulation (DES) since its inception in the nineteen-sixties, while it has been neglected and is still considered an advanced topic in the field of Business Process Modeling (BPM). The concept of resource-constrained activities is at the center of both DES and BPM. But both fields have developed different, and even incompatible, concepts of business process simulation.In the DES paradigm of Processing Networks, Gordon (1961) has introduced the resource management operations Seize and Release in the simulation language GPSS for allocating and de-allocating (releasing) resources. Thus, GPSS has established a standard modeling pattern for resource-constrained activities, which has become popular under the name of Seize-Delay-Release indicating that for simulating a resource-constrained activity, its resources are first allocated, and then, after some delay (representing the duration of the simulated activity), they are de-allocated (released).
Resource roles, process owners and resource pools
As an illustrative example, we consider a hospital consisting of medical departments where patients arrive for getting a medical examination performed by a doctor. A medical examination, as an activity, has three participants: a patient, a medical department, and a doctor, but only one of them plays a resource role: doctors. This can be indicated in an OE Class Diagram by using the stereotype «resource role» for categorizing the association ends that represent resource roles, as shown in Figure 3-3.
Notice that both the event type patient arrivals and the activity type examinations have a (mandatory functional) reference property process owner. This implies that both patient arrival events and examination activities happen at a specific medical department, which is their process owner in the sense that it owns the process types composed of them. A process owner is called "Participant" in BPMN (in the sense of a collaboration participant) and visually rendered in the form of a container rectangle called "Pool".
In Figure 3-3, the resource role of doctors corresponds to the performer role. In BPMN, Performer is considered to be a special type of resource role. According to (BPMN 2011), a performer can be "a specific individual, a group, an organization role or position, or an organization".[1]In BPMN, the performer role is specialized into the HumanPerformer of an activity, which is, in turn, specialized into PotentialOwner denoting the "persons who can claim and work" on an activity of a given type. "A potential owner becomes the actual owner [...] by explicitly claiming" an activity. Allocating a human resource to an activity by leaving the choice to those humans that play a suitable resource role is characteristic for workflow management systems, while in traditional DES approaches to resource handling, as in Arena and AnyLogic, (human) resources are assigned to a task (as its performer) based on certain policies.
One of the main reasons for considering certain objects as resources is the need to collect utilization statistics (either in an operational information system, like a workflow management system, or in a simulation model) by recording the use of resources over time (their utilization) per activity type. By designating resource roles in information models, these models provide the information needed in simulations and information systems for automatically collecting utilization statistics.
In the hospital example, a medical department, as the process owner, is the organizational unit that is responsible for reacting to certain events (here: patient arrivals) and managing the performance of certain processes and activities (here: medical examinations), including the allocation of resources to these processes and activities. For being able to allocate resources to activities, a process owner needs to manage resource pools, normally one for each resource role of each type of activity (if pools are not shared among resource roles). A resource pool is a collection of resource objects of a certain type. For instance, the three X-ray rooms of a diagnostic imaging department form a resource pool of that department.
Resource pools can be modeled in an OE Class Diagram by means of special associations between object classes representing process owners (like medical departments) and resource classes (like doctors), where the association ends, corresponding to collection-valued properties representing resource pools, are stereotyped with «resource pool», as shown in Figure 3-3. At any point in time, the resource objects of a resource pool may be out of order (like a defective machine or a doctor who is not on schedule), busy or available.
A process owner has special procedures for allocating available resources from resource pools to activities. For instance, in the model of Figure 3-3, a medical department has the procedure "allocate a doctor" for allocating a doctor to a medical examination. These resource allocation procedures may use various policies, especially for allocating human resources, such as first determining the suitability of potential resources (e.g., based on expertise, experience and previous performance), then ranking them and finally selecting from the most suitable ones (at random or based on their turn). See also (Arias et al 2018).
The conceptual process model shown in Figure 3-4 is based on the information model above. It refers to a medical department as the process owner, visualized in the form of a Pool container rectangle, and to doctor objects, as well as to the event type patient arrivals and to the activity type examinations.
This process model describes two causal regularities in the form of the following two event rules, each stated with two bullet points: one for describing all the state changes and one for describing all the follow-up events brought about by applying the rule.
When a new patient arrives:
- if a doctor is available, then she is allocated to the examination of that patient; otherwise, a new planned examination is queued up;
- if a doctor has been allocated, then start an examination of the patient.
When an examination is completed by a doctor:
- if the queue of planned examinations is empty, then the doctor is released;
- otherwise, the next planned examination by that doctor is scheduled to start immediately.
These conceptual event rules describe the real-world dynamics of a medical department according to business process management decisions. Changes of the waiting line and (de-)allocations of doctors are considered to be state changes (in the, not necessarily computerized, information system) of the department, as they are expressed in Data Object rectangles, which represent state changes of affected objects caused by an event in DPMN.
Notice that the model of Figure 3-4 abstracts away from the fact that after allocating a doctor, patients first need to walk to the room before their examination can start. Such a simplification may be justified if the walking time can be neglected or if there is no need to maximize the productive utilization of doctors who, according to this process model, have to wait until the patient arrives at the room. Below, this model is extended for allowing to allocate rooms and doctors such that patients have to wait for doctors, and not the other way around.
Switching roles: doctors as patients
The same person who is a doctor at a diagnostic imaging department may be treated as a patient of that department. It's a well-known fact that in the real world people may switch roles and may play several roles at the same time, but many modeling approaches/platforms fail to admit this. For instance, the simulation language (SIMAN) of the well-known DES modeling tool Arena does not treat resources and processing objects ("entities") as roles, but as strictly separate categories. This language design decision was a meta-modeling mistake, as admitted by Denis Pegden, the main creator of SIMAN/Arena, in (Drogoul et al 2018) where he says "it was a conceptualization mistake to view Entities and Resources as different constructs".
In Figure 3-5, the above model is extended by categorizing the classes doctors and patients as «role type» classes and adding the «kind» class people as a supertype of doctors and patients, we create the possibility that a person may play both roles: the role of a doctor and the role of a patient, albeit not at the same time. The object type categories «kind» and «role type» have been introduced to conceptual modeling by Guizzardi (2005).
Queueing planned activities
Whenever an activity is to be performed but cannot start due to a required resource not being available, the planned activity is placed in a queue as a waiting job. Thus, in the case of a medical examination of a patient, as described in the model of Figure 3-5, the waiting line represents, in fact, a queue of planned examinations (involving patients), and not a queue of waiting patients.
This consideration points to a general issue: modeling resource-constrained activities implies modeling queues of planned activities, while there is no need to consider (physical) queues of (physical) objects. Consequently, even if a real-world system includes a physical queue (of physical objects), an OEM-A model may abstract away from its physical character and consider it as a queue of planned activities (possibly including pre-allocated resources). While a physical queue implies that there is a maximum capacity, a queue of planned activities does not imply this. For instance, when a medical department does not require patients to queue up in a waiting area for obtaining an examination, but accepts their registration for an examination by phone, the resulting queue of waiting patients is not a physical queue (but rather a queue of planned examinations) and there is no need to limit the number of waiting patients in the same way as in the case of queuing up in a waiting area with limited space.
A planned activity can only start, when all required resources have been allocated to it. Thus, a planned examination of a patient can only start, when both a room and a doctor have been allocated to it. Let's assume that when a patient p arrives, only a room is available, but not a doctor. In that case, the available room is allocated to the planned examination, which is then placed in a queue since it still has to wait for the availability of a doctor. Only when a doctor becomes available, e.g., via the completion of an examination of another patient or via an arrival of a doctor, the doctor can be allocated as the last resource needed to start the planned examination of patient p.
As a consequence of these considerations, the waiting line of a medical department modeled in Figure 3-5 as an ordered collection of patients is renamed to planned walks in Figure 3-6. In addition, a property planned examinations, which holds an ordered collection of patient-room pairs, is added to the class medical departments. These model elements reflect the hospital's business process practice to maintain a list of patients waiting for the allocation of a room to walk to and a list of planned examinations, each with a patient waiting for a doctor in an examination room.
Decoupling the allocation of multiple resources
For being more realistic, we consider the fact that patients first need to be walked by nurses to the room allocated to their examination before the examination can start. Thus, in the model of Figure 3-6, we add a second activity type, walks to room, involving people (typically, nurses and patients) walking to an examination room.
This process model describes three causal regularities in the form of the following three event rules:
When a new patient arrives:
- if a room and a nurse are available, they are allocated to the walk of that patient to that room, otherwise a new planned walk is placed in the corresponding queue;
- if a room has been allocated, then the nurse starts walking the patient to the room.
When a walk of a patient and nurse to a room is completed:
- if there is still a planned walk in the queue and a room is available, then the room is allocated and the nurse is re-allocated to the walk of the next patient to that room.
if a doctor is available, she is allocated to the examination of that patient, else a new planned examination of that patient is queued up; - if a doctor has been allocated, then the examination of that patient starts
if the nurse has been re-allocated, she starts walking the next patient to the allocated room.
- if there is still a planned walk in the queue and a room is available, then the room is allocated and the nurse is re-allocated to the walk of the next patient to that room.
When an examination of a patient is completed by a doctor in a particular room:
- if there is still a planned examination (of another patient in another room), then re-allocate the doctor to that planned examination, else release the doctor;
if the waiting line is not empty, re-allocate the room to the next patient, else release the room; - if the doctor has been re-allocated to a planned examination, that examination starts;
if the room has been re-allocated to another patient, that patient starts walking to the room.
- if there is still a planned examination (of another patient in another room), then re-allocate the doctor to that planned examination, else release the doctor;
Notice that the process type described in Figure 3-7 does not consider the fact that doctors have to walk to the examination room too, which could be modeled by adding a doctors' walks to room Activity rectangle after the patients' walks to room Activity rectangle.
For being able to collect informative utilization statistics, it is required to distinguish the total time a resource is allocated (its 'gross utilization') from the time it is allocated for productive activities (its 'net utilization'). Thus, only examinations would be classified as productive activities, while walks to room would rather be considered a kind of set-up activities.
Re-engineering the process type by centralizing the re-allocation of resources
In the process type described in Figure 3-7, the re-allocation of released resources is handled in the event rules of activity end events:
- when a nurse's and patient's walk to a room ends, the nurse is free to be re-allocated; so if there is another planned walk and a room is available, the nurse is re-allocated to a walk of the next patient to that room;
- when an examination ends, its resources (a doctor and a room) are re-allocated, if planned activities are waiting for them.
This approach requires that the same re-allocation logic is repeated in the event rules of all activity types associated with that type of resource, implying that all performers involved would have to know and execute the same re-allocation logic. It is clearly preferable to centralize this logic in a single event rule, which can be achieved by introducing release resource request events following activities that do not need to keep resources allocated, as shown in Figure 3-8 where the re-allocation of doctors and rooms is decoupled from the examination activities and centralized (e.g., in a special resource management unit) by adding the two event types room release requests and doctor release requests modeling simultaneous events that follow examinations.
This process model describes an improved business process with six event rules:
When a new patient arrives:
- if a room and a nurse are available, they are allocated to the walk of that patient to that room, otherwise a new planned walk is placed in the corresponding queue;
- if a room has been allocated, then the nurse starts walking the patient to the room.
When a walk of a patient and nurse to a room is completed:
- if a doctor is available, she is allocated to the examination of that patient, else a new planned examination of that patient is queued up;
- if a doctor has been allocated, then the examination of that patient starts; in addition, a nurse release request is issued.
When a nurse release request has been issued:
- if the waiting line is not empty and a room is available, allocate the room and re-allocate the nurse to the next patient, else release the nurse;
- if the nurse has been re-allocated to another patient, she starts walking that patient to the room.
When an examination is completed:
- [no state change]
- a room release request is issued (e.g., by notifying a resource management clerk or the department's information system), and, in parallel, a doctor release request is issued.
When a room release request is received by a resource manager:
- if the waiting line is not empty and a nurse is available, allocate the nurse and re-allocate the room to the next patient, else release the room;
- if the room has been re-allocated to another patient, the nurse starts walking that patient to the room.
When a doctor release request is received by a resource manager:
- if there is still a planned examination (of another patient in another room), then re-allocate the doctor to that planned examination, else release the doctor;
- if the doctor has been re-allocated to a planned examination, that examination starts.
Notice that, in the general case, instead of scheduling several simultaneous release requests, each for a single resource, when an activity completes, a single joint release request for all used resources should be scheduled, allowing to re-allocate several of the released resources jointly.
Displaying the process owner and activity performers
The process owner and the involved performers can be displayed in an OEM process model by using a rectangular Pool container for the process owner and Pool partitions called Lanes for the involved activity performers, as shown in Figure 3-9. Notice that, as opposed to BPMN, where lanes do not have a well-defined meaning, but can be used for any sort of arranging model elements, DPMN Lanes represent organizational actors playing the resource role of performer.
Non-exclusive resources
In OEM, a resource is exclusive by default, that is, it can be used in at most one activity at the same time, if no parallel participation multiplicity is specified. For instance, in all information models above (e.g., in Figure 3-3), the participation associations between the resource classes rooms and doctors and the activity classes walks to room and examinations do not specify any parallel participation multiplicity (for the association end at the side of the activity class), but just the common (historical participation) multiplicity of "*" expressing that resources participate in zero or more activities over time (without an upper bound).
OEM extends UML Class Diagrams by adding the association end stereotype «parallel» for expressing parallel participation multiplicities.
A non-exclusive resource can be simultaneously used in more than one activity. The maximum number of activities, in which a non-exclusive resource can participate at the same time, is normally specified at the type level for all resource objects of that type using the upper bound of a parallel participation multiplicity. In general, there may be cases where it should be possible to specify this at the level of individual resource objects. For instance, larger examination rooms may accommodate more examinations than smaller ones.
A resource can be exclusive with respect to all types of activities (which is the default case) or it can be exclusive with respect to specific types of activities. For instance, in the model of Figure 3-10, a parallel participation multiplicity of 0..1 is defined both for the participation of rooms in walks and in examinations. This means a room can participate in at most one walk and in at most one examination at the same time, which is a different business rule, allowing to walk patients to a room even if it is currently used for an examination, compared to the model of Figure 3-3, allowing to walk patients to a room only if it is currently not being used for an examination.
3.2. Resource-Constrained Activities in Simulation Design Models
In simulation design models, resource-constrained activities can be modeled in two ways:
- either abstracting away from the structure of resource object types and individual resource objects, and only representing a resource object type in the form of a named resource pool with a quantity (or counter) attribute holding the number of available resources, or
- explicitly representing resource object types and individual resource objects of that type as members of a collection representing a resource pool.
While the first approach is simpler, the second approach allows modeling various kinds of non-availability of specific resources (e.g., due to failures or due to not being in the shift plan).
For any resource object type Res, the three operations described in the following table are needed.
| Resource management operation | General meaning | Resource counter approach | Resource pool approach |
|---|---|---|---|
| isResAvailable | test if a resource of type Res is available and return true or false | test if the corresponding resource counter attribute has a value that is greater than 0 | test if the number of available resource objects in the resource pool is greater than 0 |
| allocateRes | allocate a resource object of type Res | decrement resource counter attribute | select (and return) a resource object from the set of available resource objects in the resource pool (using an allocation policy) and designate it as BUSY |
| releaseRes | de-allocate a resource object of type Res | increment resource counter attribute | take a resource object of type Res as argument and designate it as AVAILABLE |
In both approaches, it is natural to add these operations to the object type representing the process owner of the activities concerned, as in the models shown in Figure 3-11 and Figure 3-13.
In the first approach, for each resource object type in the conceptual model, a resource counter attribute is added to the object type representing the process owner and the conceptual model's resource object types are dropped.
In the second approach, the conceptual model's resource object types are elaborated by adding an enumeration attribute status holding a resource status value such as AVAILABLE or BUSY. For each resource object type, a collection-valued property (such as rooms or doctors) representing a resource pool is added to the object type representing the process owner.
A simple model with resource counters
Using the conceptual information model shown in Figure 3-3 as a starting point, we first rename all classes and properties according to OO naming conventions and replace each of the two (conceptual) operations allocate a room and allocate a doctor with a triple of isAvailable/allocate/release operations for the two resource object classes Room and Doctor in the MedicalDepartment class, where we also add the counter attributes nmrOfRooms and nmrOfDoctors. Then, the two resource object classes Room and Doctor are dropped. The result of this elaboration is the information design model shown in Figure 3-11.
Using the conceptual process model shown in Figure 3-4 as a starting point and based on the type definitions of the information design model of Figure 3-11, we get the following process design.
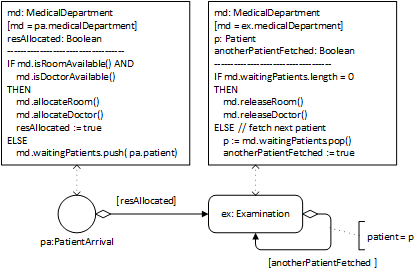
This process model defines the following two event rules.
| ON pa: PatientArrival |
|---|
| md : MedicalDepartment resAllocated : Boolean md := pa.medicalDepartment |
| IF md.isRoomAvailable() AND md.isDoctorAvailable() THEN md.allocateRoom(); md.allocateDoctor(); resAllocated := true ELSE md.waitingPatients.push( pa.patient); resAllocated := false |
| IF resAllocated SCHEDULE Examination( patient:=pa.patient, medicalDepartment:=md) |
| ON ex: Examination |
|---|
| md : MedicalDepartment anotherPatientFetched : Boolean p: Patient md := ex.medicalDepartment |
| IF md.waitingPatients.length = 0 THEN md.releaseRoom(); md.releaseDoctor(); anotherPatientFetched := false ELSE p := md.waitingPatients.pop(); anotherPatientFetched := true |
| IF anotherPatientFetched SCHEDULE Examination( patient:=p, medicalDepartment:=md) |
Notice that the event scheduling arrows of Figure 3-12, and also the SCHEDULE statements of the corresponding event rule tables, do not contain assignments of the duration of activities, since it is assumed that, by default, whenever an activity type has an operation duration(), the duration of activities of this type are assigned by invoking this operation.
A general model with resource objects as members of resource pools
In a more general approach, instead of using resource counter attributes, explicitly modeling resource object classes (like Room and Doctor) allows representing resource roles (stereotyped with «res») and resource pools (stereotyped with «pool») in the form of collections (like md.rooms and md.doctors) and modeling various forms of non-availability of resources (such as machines being defective or humans not being in the shift plan) with the help of corresponding resource status values (such as OUT_OF_ORDER). The result of this elaboration is the information design model shown in Figure 3-13.
For an OEM-A class model, like the one shown in Figure 3-13, the following completeness constraint must hold: when an object type O (like Doctor) participates in a «res» association (a resource role association) with an activity type A (like Examination), the process owner object type of A (MedicalDepartment) must have a «pool» association with O.
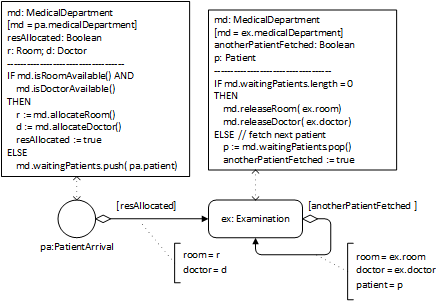
Extending OE Class Diagrams by adding a «resource type» category
The information design model of Figure 3-13 contains two object types, Room and Doctor, which are the range of resource role and resource pool properties (association ends stereotyped «res» and «pool»). Such object types can be categorized as «resource type» with the implied meaning that they inherit a resource status attribute from a pre-defined class Resource, as shown in Figure 3-16.
ResourceThe introduction of resource types to OEM class models allows simplifying models by dropping the following modeling items from OEM-A class models, making them part of the implicit semantics:
- the status attributes of object types representing resource types, which are implicitly inherited;
- the pre-defined enumeration ResourceStatusEL;
- the resource management operations isAvailable, allocate and release, which are implicitly inherited by any resource type; and
- the planned activity queues may possibly be implicitly represented for any resource-constrained activity type in the form of ordered multi-valued reference properties of its process owner object type.
Revisiting the manufacturing workstation example
A manufacturing workstation, or a "server" in the terminology of Operation Research, represents a resource for the processing activities performed at/by it. This was left implicit in the OEM-A class model shown on the right-hand side of Figure 2-3. Using the new modeling elements (resource types, resource roles and resource pools), the processing activities of a workstation can be explicitly modeled as resource-constrained activities, leading to the OEM-A class model shown in Figure 3-17 and to a more high-level and more readable process model compared to the process model of Figure 2-4.
Decoupling the allocation of multiple resources
In a simplified simulation design for the extended scenario (with patients and nurses first walking to examination rooms before doctors are allocated for starting the examinations) described by the conceptual models of Figure 3-6 and Figure 3-9, we do not consider the walks of doctors, but only the walks of nurses and patients. For simplicity, we drop the superclass people and associate the activity type WalkToRoom with the Patient and Nurse classes. The result of this elaboration is the information design model shown in Figure 3-18.
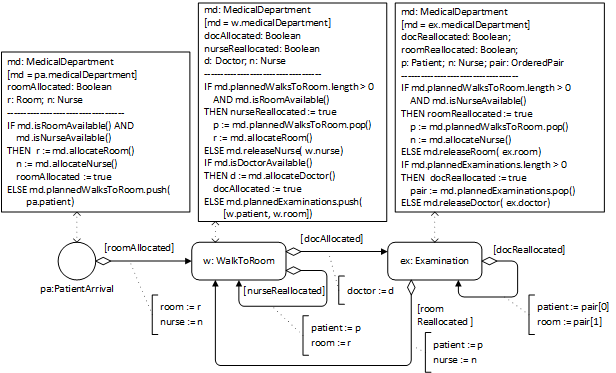
This process design model defines three event rules. Notice that the Examination event rule either re-allocates the doctor to the next planned examination and schedules it, if there is one, or it releases the doctor and re-allocates the room to the next planned walk-to-room and schedules it, if there is one.
Centralizing the re-allocation of resources
As shown before, in the conceptual process models of Figure 3-8 and Figure 3-9, the re-allocation of resources can be centralized with the help of resource release request events and the process owner and the involved performers can be displayed by using a Pool that is partitioned into Lanes for the involved activity performers, resulting in the model shown in Figure 3-20.
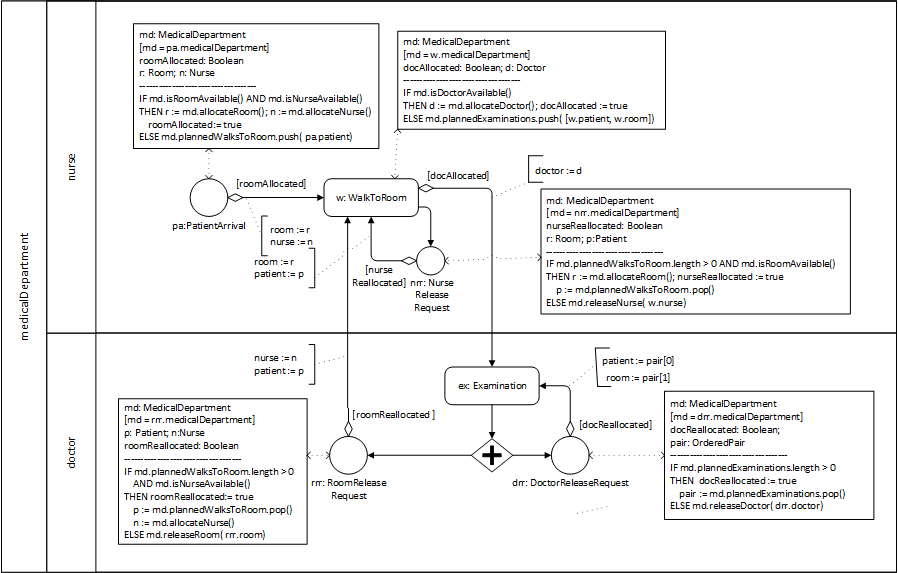
3.3. The Allocate-Release Modeling Pattern
The conceptual process model shown in Figure 3-9 and the process design model shown in Figure 3-20 exhibit a general pattern for modeling a sequence of two resource-constrained activities of types A1 and A2 shown in Figure 3-21. For describing this pattern, we assume that
- the process owner maintains queues for planned activities: q1 for for planned activities of type A1, and q2 for planned activities of type A2, both defined as queue-valued (i.e., ordered multi-valued) reference properties of the process owner in the underlying information model;
- the underlying information model specifies the sets of resources R1 and R2 required by A1 and A2,
- the set of resources required by A2 but not by A1 is denoted by R2−R1;
- the set of resources required by A1 and by A2 is denoted by R1∩R2.
We can describe the algorithm of the Allocate-Release Modeling Pattern for the case of a sequence of two resource-constrained activities in the following way:
- ON start event:
- If the resources R1 required by A1 are available, they are allocated; otherwise, a planned A1 activity is added to the queue q1.
- If the resources R1 have been allocated, a new activity of type A1 is started.
- WHEN an activity of type A1 completes:
- The resources R2−R1 are allocated, if they are available; otherwise, a planned A2 activity with reserved resources R1∩R2 is added to q2.
- If R2−R1 have been allocated, a new activity of type A2 is started. In addition, an immediate release request for R1−R2 is caused/scheduled.
- ON release request for R1−R2:
- If q1 is not empty and the resources R1∩R2 required by both A1 and A2 are available, they are allocated and R1−R2 are re-allocated to head( q1); otherwise, R1−R2 are released.
- If the resources R1−R2 have been re-allocated, a new activity of type A1 is started.
- WHEN an activity of type A2 completes:
- There is no state change.
- An immediate release request for R2 is caused/scheduled.
- ON release request for R2:
- If R1∩R2 is nonempty: if q1 is not empty and the resources R1−R2 required by A1, but not yet allocated, are available, they are allocated and R1∩R2 are re-allocated to head( q1); otherwise, R1∩R2 are released. If q2 is not empty, then re-allocate R2−R1 to head( q2); otherwise, R2−R1 are released.
- If R1∩R2 have been re-allocated, a new activity of type A1 is started. If R2−R1 have been re-allocated, a new activity of type A2 is started.
New modeling elements for expressing the Allocate-Release Modeling Pattern
Since the Allocate-Release Modeling Pattern defines a generic algorithm for allocating and releasing resources, its (pseudo-)code does not have to be included in a DPMN Process Diagram, but can be delegated to an OE simulator supporting the resource-dependent scheduling of resource-constrained activities according to this pattern. This approach allows introducing new DPMN modeling elements for expressing the Allocate-Release Modeling Pattern in a concise way, either leaving allocate-release steps completely implicit, as in the DPMN Process Diagram of Figure 3-22, or explicitly expressing them, as in Figure 3-23.
The most important new DPMN modeling element introduced are resource-dependent causation (resp., activity start) arrows pointing to resource-constrained activities, as in Figure 3-22. These arrows are high-level modeling elements representing the implicit allocate-release logic exhibited in Figure 3-21. Thus, the meaning of the model of Figure 3-22 is provided by the model of Figure 3-21.
It is an option to display the implicit allocate-release steps with Allocate and Release rectangles together with simple control flow arrows, as between the start event circle and the Allocate R1 rectangle in Figure 3-23.
The meaning of the model of Figure 3-23 is the same as that of Figure 3-22, which is provided by the model of Figure 3-21. The fact that, using resource-dependent activity start arrows, the allocate-release logic of resource-constrained activities does not have to be explicitly modeled and displayed in an OEM process model shows the power of founding a process model on an information model, since the entire resource management logic can be expressed in terms of resource roles, constraints and pools in an OEM information model. This is in contrast to the common approach of industrial simulation tools, such as Simio and AnyLogic, which require defining resource roles, constraints and pools as well as explicit allocate-release steps in the process model, in a similar way as shown in Figure 3-23.
Using resource-dependent activity start arrows in a process model implies using their standard allocate-release logic according to which required resources that have not been allocated before are allocated immediately before an activity requiring them is started and released immediately after this activity is completed if they are not required by the next activity. Whenever another (non-standard) resource allocation logic is needed, it has to be expressed explicitly using ordinary event scheduling arrows.
Simplifying the workstation process model
We can now simplify the workstation model using the resource type category for WorkStation in the OEM class model and a resource-dependent activity start arrow from the arrival event to the processing activity in the DPMN process model. The resulting class model is shown in Figure 3-26.
The simplification of the process model of Figure 2-5 results in the model of Figure 3-25.
Simplifying the medical department process model
We can now simplify the medical department model using the resource type category for Doctor, Room and Nurse in the OEM class model and resource-dependent activity start arrows in the DPMN process model. The resulting class model is shown in Figure 3-26.
The simplification of the rather complex process model of Figure 3-20 by using resource-dependent activity start arrows results in the model of Figure 3-27.
3.4. Organization Modeling Concepts
The activities of a business process are typically performed by human resources holding certain organizational positions and playing certain organizational roles within an organization or organizational unit. It should, therefore, not come as a surprise that Activity-Based DES modeling requires to consider a number of organization modeling concepts. In particular, the concept of resource roles and the related concepts of organizational roles and organizational positions are paramount to Activity-Based DES modeling.
Many resource management concepts, such as resource roles, including performer roles, and resource pools, can be captured in information models in the form of categorized ("stereotyped") UML class modeling elements such as «rr» for resource role association ends, «pr» for performer role association ends, and «rp» for resource pool association ends, leading to an extension of UML Class Diagrams, called OE Class Diagrams, such as the following one:
This conceptual OE class model describes two activity types, "walks to rooms" and "examinations", each one associated with
- the object type "medical departments", providing the (business) process owner;
- a performer object type ("nurses" and "doctors") via a performer role («pr») association end, providing the activity performer (as a special type of resource);
- another resource object type via a resource role («rr») association end, providing another resource of each activity (a "room");
In addition, the model describes three types of resource pools by means of «rp» association ends, such that each resource pool is associated with a process owner maintaining the pool and providing the resources corresponding to one of the three resource roles.
Notice that in a conceptual OE class model, each activity type should have a performer role («pr») association, while in an OE class design model (being part of a simulation design model), it is an option to abstract away from the distinction of performers among the resources of an activity and simply consider all its resources (including its performer) as plain resources. This is common in management science and Operations Research, where the main interest is in obtaining general performance statistics for resources, such as their utilization, no matter if they are human resources (performers) or not.
We show how further organization modeling concepts can be introduced to OEM&S.
Refining Object Types to Resource (Role) Types and Performer (Role) Types
While a resource role denotes an association end, corresponding to a reference property, a resource (or performer) role type denotes an object type that is the range of a resource (or performer) role. For simplicity, we say "resource type" (or "performer type") instead of "resource role type" (or "performer role type").
For all «object type» classes of an OE class model that are the range of a performer role or a resource role, it may be an option to replace their «object type» category with a «performer type» or «resource type» category, as shown for the object types "nurses", "doctors" and "rooms" in the following refined model:
Notice that typically each resource type is the range of one resource role and represents a resource pool for it. A resource type may be the target class of more than one resource role association end and its population may be partitioned into several resource pools such that at least one pool is assigned to each resource role.
However, the replacement of the «object type» category of a class with a (performer or resource) role type category is only an option, if all instances of the class are playing that role. In the above example, if there are doctors who do not perform examinations (but only surgical operations), then the object type "doctors" cannot be turned into a performer type "doctors". In any case, it may be turned into an organizational position, as explained in the next section.
Refining Performer Types to Organizational Positions
An organizational position is defined by a name and a set of performer types representing the roles (or responsibilities) of the position holders. For instance, in a medical department, the organizational position Nurse may be defined by the set of performer types Guide and ExaminationAssistant, where a Guide is required for guiding a patient to an examination room and an ExaminationAssistant is required for assisting a doctor in a medical examination.
Computationally, an organizational position is an object type that is partitioned into (one or more) performer types, implying that its instances (position holders) are human resources that can be allocated for performing any corresponding activity.
For instance, the organizational position Nurse is partitioned into the performer types Guide and ExaminationAssistant, with the meaning that nurses may play the role of guides or the role of examination assistants.
In simple cases, an organizational position is defined by just one performer type.
In an Activity-Based DES model, for each organizational position (like Clerk) consisting of the performer roles p1,...,pn, there is a default resource pool, or better: performer pool, (like clerks) that includes all employees holding that position. This pool will be used for allocating the performers of activities with a performer role pi.
These considerations lead to the following refined version of the medical department model shown in the diagram above:
Notice that in this refined model, we have also categorized the object type "patients" as «person role type» and the object type "medical departments" as «organizational unit type».
Chapter 4. Processing Activities and Processing Networks
A Processing Activity is a resource-constrained activity that takes one or more objects as inputs and processes them in some way (possibly transforming them). The processed objects have been called "transactions" in GPSS and "entities" in SIMAN/Arena, while they are called processing objects in DPMN.
Ontologically, there are one or more objects participating in an activity, as shown in Figure 4-1. Some of them represent resources, while others represent processing objects. For instance, in the information and process models of a medical department shown in Figure 3-6 and Figure 3-9, there are two processing activity types: walks to room and examinations. In walks to room, since nurses are walking patients to examination rooms, nurses and rooms are resources, while patients are processing objects. In examinations, doctors and rooms are resources, while patients are processing objects. If patients would walk to an examination room by themselves (without the help of a nurse), patients would be the performers of walks to a room, and not processing objects, and, consequently, walks to a room would not be processing activities.
Processing activities typically require immobile physical resources, like rooms or workstation machines, which define the inner nodes of a Processing Network (PN). A Processing Object enters such a network via an Arrival event at an Entry Node, is subsequently routed along a chain of Processing Nodes where it is subject to Processing Activities, and finally exits the network via a Departure event at an Exit Node.
The nodes of a PN define locations in a network space, which may be based on a two- or three-dimensional Euclidean space. Consequently, OEM-PN models are spatial simulation models, while basic OEM and OEM-A allow to abstract away from space. When processing objects are routed to a follow-up processing activity, they move to the location of the next processing node. The underlying space model allows visualizing a PN simulation in a natural way with processing objects as moving objects.
Each node in a PN model represents both an object and an event type. An Entry Node represents both an entry point (e.g., a reception area or an entrance to an inventory) and an arrival event type. A Processing Node represents both a resource object (e.g., a workstation or a room) and a processing activity type. An Exit Node represents both an exit point and a departure event type. A flow arrow connecting two Processing Nodes represents both an event flow and an object flow. Thus, the node types and the flow arrows of a PN are high-level modeling concepts that are overloaded with two meanings.
A PN modeling language should have elements for modeling each of the three types of nodes. Consequently, DPMN-A has to be extended by adding new visual modeling elements for entry, processing and exit nodes, and for connecting them.
In the field of DES, PNs have often been characterized by the narrative of “entities flowing through a system”. In fact, while in basic DPMN and in DPMN-A, there is only a flow of events, in DPMN-PN this flow of events is over-laid with a flow of (processing) objects.
PNs have been investigated in operations management and the mathematical theory of queuing (Loch 1998, Williams 2016) and have been the application focus of most industrial simulation software products, historically starting with GPSS (Gordon 1961) and SIMAN/Arena (Pegden and Davis 1992). They allow modeling many forms of discrete processing processes as can be found, for instance, in the manufacturing industry and the services industry.
It is remarkable that the PN paradigm has dominated the discrete event simulation market since the 1990’s and still flourishes today, mainly in the manufacturing and services industries, often with object-oriented and “agent-based” extensions. Its dominance has led many simulation experts to view it as a synonym of DES, which is a conceptual flaw because the concept of DES, even if not precisely defined, is clearly more general than the PN paradigm.
The PN paradigm has often been called a “process-oriented” DES approach. But unlike the business process modeling language BPMN, it is not concerned with a general concept of business process models, but rather with the special class of processing process models for discrete processing systems. A processing process includes the simultaneous handling of several “cases” (processing objects) that may compete for resources or have other interdependencies, while a “business process” in Business Process Management has traditionally been considered as a case-based process that is isolated from other cases.
For PN models, a simulator can automatically collect the following statistics, in addition to the resource-constrained activities statistics described in 3. Resource-Constrained Activities:
- The number of processing objects that arrived at, and departed from, the system.
- The number of processing objects in process (that is, either waiting in a queue/buffer or being processed)
- The average time a processing object spends in the system (also called throughput time).
During a simulation run, it must hold that the number of processing objects that arrived at the system is equal to the sum of the number of processing objects in process and the number of processing objects that departed from the system, symbolically:
4.1. Conceptual Modeling of Processing Networks
For accommodating PN modeling, OEM-A is extended by adding pre-defined types for processing objects, entry node objects, arrival events, processing node objects, processing activities, exit objects and departure events, resulting in OEM-PN. These "built-in" types, which are described in Figure 4-2, allow making PN models based on them simply by making a process model (with DPMN) without the need of making an information/class model as its foundation, as shown in Figure 4-3.
An example of a conceptual PN model: Department of Motor Vehicles
As a simple example of a PN simulation model we consider a Department of Motor Vehicles (DMV) with two consecutive service desks: a reception desk and a case handling desk. When a customer arrives at the DMV, she first has to queue up at the reception desk where data for her case is recorded. The customer then goes to the waiting area and waits for being called by the case handling desk where her case will be processed. After completing the case handling, the customer leaves the DMV via the exit.
Customer arrivals are modeled with an «entry node» element (with name “DMV entry”), the two consecutive service desks are modeled with two «processing node» elements, and the departure of customers is modeled with an «exit node» element (with name “DMV exit”).
DPMN is extended by adding the new modeling elements of PN Node rectangles, representing node objects, and PN Object Flow arrows, representing combined object-event flows. PN Node rectangles take the form of stereotyped UML object rectangles, while PN Object Flow arrows have a special arrow head consisting of a circle and three bars, as shown in Figure 4-3.
Using both Object Flow arrows and Event Scheduling arrows
While an Object Flow arrow between two nodes implies both a flow of the processing object to the successor node and the resource-dependent scheduling of the next processing activity, an Event Scheduling arrow from a processing node to an Event circle represents an event flow where a processing activity end event causes/schedules another event, as illustrated in the example of Figure 4-4.
4.2. Processing Network Design Models
For accommodating PN modeling, OEM-A is extended by adding pre-defined types for processing objects, entry node objects, arrival events, processing node objects, processing activities, exit objects and departure events, resulting in OEM-PN. These "built-in" types, as described in Figure 4-5, allow making PN models based on them simply by making a process model with DPMN without the need of making an OEM class model as its foundation, as shown in Figure 4-6.
Notice that the range of the properties arrivalRecurrence, successorNodes and duration of the built-in object types EntryNode and ProcessingNode is Function, which means that the value of such a property for a specific node is a specific function. While the standard UML semantics does not support such an extension of the semantics of properties in the spirit of the Functional Programming paradigm, its implementation in a functional OO programming language like JavaScript, where objects can have instance-level functions/methods, is straightforward.
The property successorNodes allows to express a function that provides, for any given entry or processing node, a (possibly singleton) set of processing nodes or exit nodes. Such a function can express several cases of routing a processing object from a node to one or more successor nodes:
- a fixed unique successor node for modeling a series of processing nodes connected by (possibly conditional) object flow arrows, as in Figure 4-8;
- a conditional unique successor node for modeling an Exclusive (XOR) Gateway leading to one of several possible successor nodes;
- a variable subset of a set of potential successor nodes for modeling an Inclusive (OR) Gateway;
- a fixed set of successor nodes for modeling a Parallel (AND) Gateway;
In a DPMN diagram, the set of successor nodes of a node is defined by Flow Arrows, possibly in combination with Gateways.
PN example 1: a single workstation
Part arrivals are modeled with an «entry node» element (with name “partEntry”), the workstation is modeled with a «processing node» element, and the departure of parts is modeled with an «exit node» element (with name “partExit”).
DPMN is extended by adding the new modeling elements of PN Node rectangles, representing node objects with associated event types, and PN Flow arrows, representing combined object-event flows. PN Node rectangles take the form of stereotyped UML object rectangles, while PN Flow arrows have a special arrow head, as shown in Figure 4-6.
PN example 2: a workstation may have to rework parts
Parts that turn out to be defective after being processed need to be reworked. This can be modeled by adding an attribute percentDefective to the object type Workstation and suitable logic to the Processing activity end event rule such that in percentDefective % of all cases a processed part cannot depart the system (i.e., is not removed from the input buffer), but is being reworked by another Processing activity.
PN example 3: Department of Motor Vehicles
A Department of Motor Vehicles (DMV) has two consecutive service desks: a reception desk and a case handling desk. When a customer arrives at the DMV, she first has to queue up at the reception desk where data for her case is recorded. The customer then goes to the waiting area and waits for being called by the case handling desk where her case will be processed. After completing the case handling, the customer leaves the DMV via the exit.
Customer arrivals are modeled with an «entry node» element (with name “dmvEntry”), the two consecutive service desks are modeled with two «processing node» elements, and the departure of customers is modeled with an «exit node» element (with name “dmvExit”).
4.3. Proprietary terminologies and diagram languages
Even after a 50 years history of PN modeling and simulation there is still no vendor-neutral language definition for the PN paradigm, e.g., in the form of a meta-model, which could be used as a basis for comparing and evaluating different PN modeling tools, and for interchanging models between them. The simulation modeling concepts of the PN paradigm, which have been pioneered by GPSS and SIMAN/Arena, have been adopted by many other simulation software products, including Simul8, Simio and AnyLogic. However, each product based on this paradigm uses its own variants of the PN concepts, together with their own proprietary terminology and proprietary diagram language, as illustrated by Table 4-1.
| OEM | Arena | Simul8 | Simio | AnyLogic |
|---|---|---|---|---|
Processing Object | Entity | Work Item | Token | Agent |
Entry Node | Create | Start Point | Source | Source |
Processing Node | Process | Queue+Activity | Server | Service or Seize+Delay+Release |
Exit Node | Dispose | End Point | Sink | Sink |
Notice especially the strange term “Agent” used by AnyLogic, instead of the Arena term “Entity”, for processing objects like manufacturing parts in production systems or patients in hospitals. It is confusing to call a manufacturing part, such as a wheel in the production of a car, an “agent”.
As noted by van der Aalst (2014), “the use of proprietary building blocks in tools such as ARENA makes it hard to interchange simulation models”.
We illustrate the problem of different proprietary diagram languages by showing an Arena diagram in Figure 4-9 and an AnyLogic diagram in Figure 4-10, both representing the DMV model of Figure 4-8.

While an Arena "Process" element, like Reception Desk in Figure 4-9, when defined with an activity of type Delay, does not require defining any explicit resources while assuming the Process element itself to be an implicit resource, an AnyLogic "Service" element, like reception in Figure 4-10, requires first defining a resource pool (with a resource type and a pool size), like receptionDesks, and then reference it in the definition of the element.
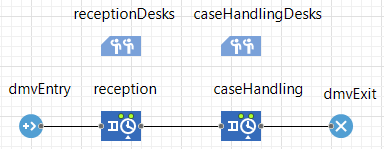
Chapter 5. Transformation Activities
A transformation activity is a processing activity that transforms one or more input objects of certain types into one ore more output objects of different types.
To be completed ...
Acknowledgements
The author is grateful to Frederic (Rick) D. McKenzie (†2020) for providing the opportunity to spend a sabbatical at the Modeling, Simulation and Visualization Engineering Department of Old Dominion University in Norfolk, Virginia, USA, in 2016. During that time, the grounds of the presented work have been laid.
This research has not been funded by the German research foundation Deutsche Forschungsgemeinschaft (DFG).
Bibliography
- van der Aalst, W.M.P. 2014. Business process simulation survival guide. In: J. vom Brocke and M. Rosemann (eds), Handbook on business process management, vol 1, 2nd edn., Springer, pp 337–370.
- Arias, M., J. Munoz-Gama, and M. Sepulveda. 2018. Towards a Taxonomy of Human Resource Allocation Criteria. In: Teniente E. and M. Weidlich (eds.), Business Process Management Workshops. BPM 2017. Lecture Notes in Business Information Processing 308, 475–483, Springer.
- Business Process Model and Notation (BPMN), Version 2.0, 2011. http://www.omg.org/spec/BPMN/2.0
- Drogoul, A., P. Fishwick, N. Gilbert, D. Pegden, G. Wagner, and L. Yilmaz. 2018. Panel Discussion: On the Unity and Diversity of Computer Simulation. Journal of Simulation Engineering, volume 1, 2018. Available from https://articles.jsime.org/1/4/Unity-and-Diversity-of-Simulation
- Gordon, G. 1961. A general purpose systems simulation program. In AFIPS '61: Proceedings of the Eastern Joint Computer Conference, Washington, D.C., 87–104, Association for Computing Machinery.
- Guizzardi, G. 2005. Ontological foundations for structural conceptual models. PhD thesis, University of Twente, Enschede, The Netherlands. CTIT Ph.D. thesis series No. 05-74 ISBN 90-75176-81-3.
- Gurevich, Y. 1985. A New Thesis. Abstracts, American Mathematical Society, 6:4, p.317.
- Loch, C.H. 1998. Operations Management and Reengineering. European Management Journal, 16, 306-317.
- Markowitz, H., B. Hausner, and H. Karr. 1962. SIMSCRIPT: A Simulation Programming Language. Report No. RM-3310-PR. Santa Monica, CA: The RAND Corporation.
- Pegden, C.D. and D.A. Davis. 1992. Arena: a SIMAN/Cinema-based hierarchical modeling system. In Proceedings of the 24th Winter Simulation Conference (WSC '92). ACM, New York, NY, USA, 390–399.
- Schruben, L.W. 1983. Simulation Modeling with Event Graphs. Communications of the ACM 26, 957-963.
- Standridge, C.R. 2013. Beyond Lean: Simulation in Practice, Second Edition, Open Access book, available from https://scholarworks.gvsu.edu/cgi/viewcontent.cgi?article=1006&context=books.
- Wagner, G. 2017a. An Abstract State Machine Semantics for Discrete Event Simulation. In Proceedings of the 2017 Winter Simulation Conference. Piscataway, NJ: IEEE. Available from https://www.informs-sim.org/wsc17papers/includes/files/056.pdf.
- Wagner, G. 2017b. Sim4edu.com – Web-Based Simulation for Education. Proceedings of the 2017 Winter Simulation Conference. Piscataway, NJ: IEEE.
- Wagner, G. 2018a. Discrete Event Process Modeling Notation (DPMN). Language Reference. Available from https://dpmn.info/spec.
- Wagner, G. 2018b. Information and Process Modeling for Simulation – Part I: Objects and Events. Journal of Simulation Engineering 1, 1–25, 2018. Available from https://articles.jsime.org/1/1.
- Williams, R.J. 2016. Stochastic Processing Networks. Annual Review of Statistics and Its Application 3:1, 323–345.
Appendix A: OEM Elements
OEM extends UML Class Diagrams by adding the categories ("stereotypes") listed in the following table.
| Name | UML stereotype | Category of | OEM language level |
|---|---|---|---|
| object type | «object type» | Class | basic OEM |
| event type | «event type» | Class | basic OEM |
| exogenous event type | «exogenous event type» | Class | basic OEM |
| random variate sampling function | «rv» | Operation | basic OEM |
| activity type | «activity type» | Class | OEM-A |
| resource role | «resource role» (in short, «rr») | Association End | OEM-A |
| resource pool | «resource pool» (in short, «rp») | Association End | OEM-A |
| parallel participation (multiplicity) | «parallel» | Association End | OEM-A |
| entry node | «entry node» | Object | OEM-PN |
| processing node | «processing node» | Object | OEM-PN |
| exit node | «exit node» | Object | OEM-PN |
A UML class model using these stereotypes is called an OE class model.
DPMN extends BPMN Process Diagrams by adding the modeling elements listed in the following table.
| Name | OEM/DPMN language level | Visual notation |
|---|---|---|
| DPMN Data Objects with event rule variable declarations and state change statements | basic DPMN | |
| Delay annotations of Event Flow arrows | basic DPMN | |
| Event property assignment annotations of Event Flow arrows | basic DPMN | |
| Resource-Dependent Activity Scheduling (RDAS) arrows pointing to a Resource-Constrained Activity | DPMN-A | |
| Object Flow arrows pointing to a Processing Node | DPMN-PN |